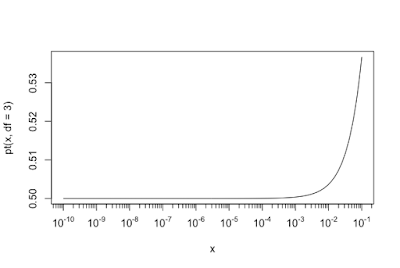
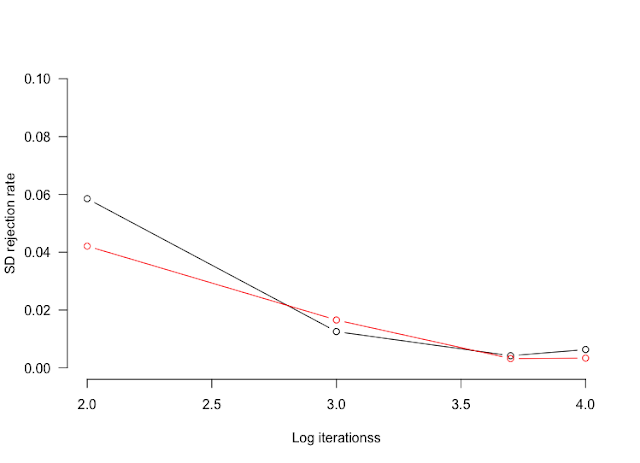
Read ... parameters in both function and interactive run
The ... parameter is very useful in a function but at the debugging stage it is boring because it generate an error in direct use. With this line, you will be able to use ... even in direct use without error: p3p <- tryCatch(list(...), error=function(e) list()) Let do some example. If you run this in interactive mode, you will get: > p3p <- tryCatch(list(...), error=function(e) list()) > p3p list() Now let use it within a function: > essai <- function(r, ...) { + p3p <- tryCatch(list(...), error=function(e) list()) + return(p3p) + } > essai() list() > essai(k=100) $k [1] 100 Original idea Marc Girondot with amelioration by Bert Gunter <bgunter.4567@gmail.com> and William Dunlap <wdunlap@tibco.com>.