Negative binomial and Poisson distributions

It is known that Poisson distribution is a special case of Negative binomial distribution. But how to parametrize NB to make it similar to Poisson in R ?

It is simple: rnbinom(n, mu=m, size=+Inf) is similar to rpois(n, lambda=m).

Try this to be sure !

layout(mat = 1:2)
x1 <- rnbinom(10000, mu=20, size =+Inf)
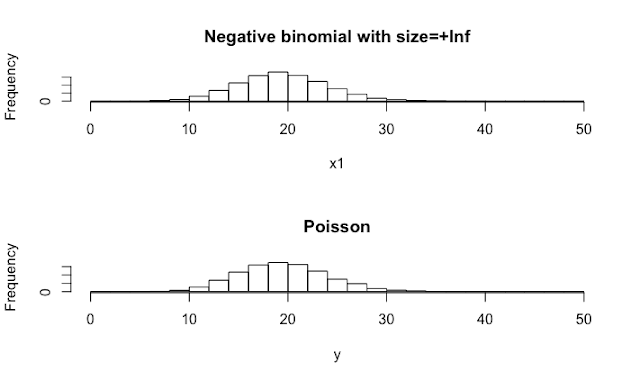
hist(x1, breaks=seq(from=0, to=50, by=2), main="Negative binomial with size=+Inf")
y <- rpois(10000, lambda=20)
hist(y, breaks=seq(from=0, to=50, by=2), main="Poisson")



Or this:

> dnbinom(x = 20, mu=20, size=+Inf)
[1] 0.08883532
> dpois(x=20, lambda=20)
[1] 0.08883532

Effect of size parameter, remember that size=+Inf is identical to Poisson distribution:

layout(mat = matrix(1:3, nrow= 1, byrow = TRUE))

 x2 <- rnbinom(10000, mu=20, size =2)
hist(x2, breaks=seq(from=0, to=150, by=2), main="Negative binomial with size=2")

 x2 <- rnbinom(10000, mu=20, size =10)
hist(x2, breaks=seq(from=0, to=150, by=2), main="Negative binomial with size=10")

 x2 <- rnbinom(10000, mu=20, size =+Inf)
hist(x2, breaks=seq(from=0, to=150, by=2), main="Negative binomial with size=+Inf")


The better flexibility of the negative binomial distribution to fit counts can be seen also in my package phenology.

> library("phenology")
> 
> gr <- add_phenology(add=Gratiot, previous = NULL, month_ref = 1, format="%d/%m/%Y", name="Cayenne2001")
Cayenne2001
Reference:  2001-01-01
> 
> # fit the data using negative binomial distribution
> 
> layout(mat = matrix(1:2, nrow= 1, byrow = TRUE))
> 
> pfixed <- c(Flat=0)
> parg <- par_init(data=gr, parametersfixed = pfixed)
> parg3 <- MinBMinE_to_Min(parg)
> 
> f <- fit_phenology(data=gr, parametersfit = parg3, parametersfixed = pfixed, 
+                    trace=0, silent=TRUE)
> outf <- plot(f, main="Negative binomial")
> 
> # fit the data using Poisson distribution
> 
> pfixed <- c(Flat=0, Theta=+Inf)
> parg <- par_init(data=gr, parametersfixed = pfixed)
> parg3 <- MinBMinE_to_Min(parg)
> 
> f1 <- fit_phenology(data=gr, parametersfit = parg3, parametersfixed = pfixed, 
+                     trace=0, silent=TRUE)
> outf1 <- plot(f1, main="Poisson")
> 
> # Compare both models
> compare_AIC(Negative.binomial=f, Poisson=f1)
[1] "The lowest AIC (1350.896) is for series Negative.binomial with Akaike weight=1.000"
                       AIC DeltaAIC Akaike_weight
Negative.binomial 1350.896   0.0000  1.000000e+00
Poisson           1741.075 390.1792  1.877852e-85
> 
> # Compare the percentage of observations out of +/- 2 SD
> print("Proportion of observations out of +/- 2 SD for negative binomial distribution")
[1] "Proportion of observations out of +/- 2 SD for negative binomial distribution"
> sum((outf[[1]]$values[, "Obs"] > outf[[1]]$values[, "Theor+2SD"]) | (outf[[1]]$values[, "Obs"] < outf[[1]]$values[, "Theor-2SD"]), na.rm=TRUE) / 
+ sum(!is.na(outf[[1]]$values[, "Obs"]))
[1] 0.04383562
> 
> print("Proportion of observations out of +/- 2 SD for Poisson distribution")
[1] "Proportion of observations out of +/- 2 SD for Poisson distribution"
> sum((outf1[[1]]$values[, "Obs"] > outf1[[1]]$values[, "Theor+2SD"]) | (outf1[[1]]$values[, "Obs"] < outf1[[1]]$values[, "Theor-2SD"]), na.rm=TRUE) / 
+   sum(!is.na(outf1[[1]]$values[, "Obs"]))
[1] 0.2082192

Commentaires

Enregistrer un commentaire

Posts les plus consultés de ce blog

Standard error from Hessian Matrix... what can be done when problem occurs

An Hessian matrix is a square matrix of partial second order derivative. From the square-root of the inverse of the diagonal, it is possible to estimate the standard error of parameters. Let take an example: val=rnorm(100, mean=20, sd=5) # Return -ln L of values in val in Gaussian distribution with mean and sd in par fitnorm<-function(par, val) {   -sum(dnorm(val, par["mean"], par["sd"], log = TRUE)) } # Initial values for search p<-c(mean=20, sd=5) # fit the model result <- optim(par=p, fn=fitnorm, val=val, method="BFGS", hessian=TRUE) # Inverse the hessian matrix to get SE for each parameters mathessian <- result$hessian inversemathessian <- solve(mathessian) res <- sqrt(diag(inversemathessian)) # results data.frame(Mean=result$par, SE=res)   library(MASS) (r<-fitdistr(val, "normal")) It works well. However, the inverse of the matrix cannot be calculated if the second order derivative for some paramete...
Lire la suite

Install treemix in ubuntu 20.04

Informations are available here  https://bitbucket.org/nygcresearch/treemix/downloads/ In terminal, enter for  Ubuntu 20.04: wget https://bitbucket.org/nygcresearch/treemix/downloads/treemix-1.13.tar.gz tar -xvf treemix-1.13.tar.gz sudo apt-get install libgsl-dev sudo apt install libboost-dev sudo apt install libboost-all-dev cd treemix-1.13/ ./configure make sudo make install And it works: $ treemix TreeMix v. 1.13 $Revision: 231 $ Options: -h display this help -i [file name] input file -o [stem] output stem (will be [stem].treeout.gz, [stem].cov.gz, [stem].modelcov.gz) -k [int] number of SNPs per block for estimation of covariance matrix (1) -global Do a round of global rearrangements after adding all populations -tf [file name] Read the tree topology from a file, rather than estimating it -m [int] number of migration edges to add (0) -root [string] comma-delimited list of populations to set on one side of the root (for migration) -g [vertices file name] [edges file na...
Lire la suite

stepAIC from package MASS with AICc

Due to a bug in dropterm() and addterm() in package MASS, it is impossible to use AICc with stepAIC() . Here is a solution. Enter these commands and now you can use: stepAIC(g0, criteria="AICc") or stepAIC(g0, criteria="BIC") For example: datax <- data.frame(y=rnorm(100), x1=rnorm(100),                     x2=rnorm(100), x3=rnorm(100), x4=rnorm(100)) g0 <- glm(y ~ x1+x2+x3+x4, data=datax) gx_AICc <- stepAIC(g0, criteria="AICc") gx_AIC <- stepAIC(g0, criteria="AIC") gx_AIC <- stepAIC(g0, criteria="BIC")
Lire la suite