Runge-Kutta algorithm
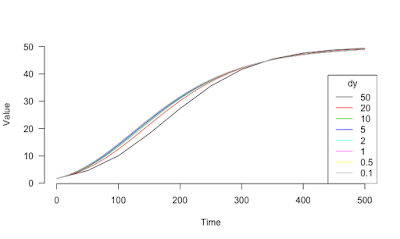
Test of the Runge-Kutta algorithm and comparison with implementation within the deSolve package or the approximation dy -> 0.
The code for Runge-Kutta algorithm has been done by Maxime Jacquemin (ESE, University Paris Sud). It does a little bit better that the deSolve code but very little.
> # from package embryogrowth
> # function lsoda wants a list
> dydt.Gompertz <- function(t, size, parms) {
+ dy.dt <- parms["alpha"]*log(parms["K"]/size)*size
+ list(dy.dt)
+ }
>
> # Same function but returns a vector
> dydt.Gompertz_2 <- function(t, size, parms) {
+ dy.dt <- parms["alpha"]*log(parms["K"]/size)*size
+ dy.dt
+ }
>
> # Integration of Gompertz function
> Gompertz <- function(x, y0, K, alpha) {
+ return(K*exp(log(y0/K)*exp(-alpha*x)))
+ }
>
> # Fonction d'intégration numérique par la méthode de Runge-Kutta
> # par Maxime Jacquemin
> Runge.Kutta <- function(y, times, func, parms = NULL)
+ {
+ n.iter <- length(times)
+ results <- rep(y, n.iter)
+ yn <- y
+
+ for (i in 2:n.iter)
+ {
+ h <- times[i] - times[i-1]
+ tn <- times[i - 1]
+ k1 <- func(tn, yn, parms)
+ k2 <- func(tn + (h / 2), yn + (h / 2) * k1, parms)
+ k3 <- func(tn + (h / 2), yn + (h / 2) * k2, parms)
+ k4 <- func(tn + h, yn + h * k3, parms)
+ yn <- yn + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)
+ results[i] <- yn
+ }
+
+ return(data.frame(times, results))
+ }
>
> xv <- seq(from=0, to =500, by=10)
> yv <- Gompertz(xv, y0=1.7, K=50, alpha=0.01)
>
> plot(x = xv,
+ y = yv,
+ type="l", bty="n", xlab="Time", ylab="Value", las=1)
> df <- data.frame(time=xv[1:6], Gompertz=yv[1:6])
>
> # using the approximation dy/dx when dx -> 0
> index <- 1
> for (dy in c(50, 20, 10, 5, 2, 1, 0.5, 0.1)) {
+ x <- seq(from=0, to =500, by=dy)
+ y <- rep(1.7, length(x))
+ for (i in 2:length(x))
+ y[i] <- y[i-1] + dydt.Gompertz_2(x[i], y[i-1], parms=c(K=50, alpha=0.01))*dy
+ dfi <- as.data.frame(list(y[match(xv[1:6], x)]), col.names=paste0("dy.", as.character(dy)))
+ df <- cbind(df, dfi)
+ lines(x, y, col=index)
+ index <- index + 1
+ # text(501, tail(y, 1)+1, as.character(dy), pos=4, xpd=TRUE)
+ }
>
> legend("bottomright", legend=as.character(c(50, 20, 10, 5, 2, 1, 0.5, 0.1)),
+ col=1:8, lty=1, title="dy")
>
> plot(x = xv,
+ y = yv,
+ type="l", bty="n", xlab="Time", ylab="Value", las=1)
>
> dy <- 10
> x <- seq(from=0, to =500, by=dy)
> rk4 <- Runge.Kutta(func = dydt.Gompertz_2,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01)
+ )
> dfi <- as.data.frame(
+ list(
+ rk4[
+ match(xv[1:6], x)
+ , 2]
+ ), col.names="rk4")
> df <- cbind(df, dfi)
>
>
> system.time(for (i in 1:10000)
+ Runge.Kutta(func = dydt.Gompertz_2,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01)
+ )
+ )
utilisateur système écoulé
19.460 0.197 19.766
> points(rk4[, 1], rk4[, 2], pch=1)
>
>
> library(deSolve)
> dy <- 10
> x <- seq(from=0, to =500, by=dy)
> rk4_desolve <- lsoda(func = dydt.Gompertz,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01))
> dfi <- as.data.frame(list(rk4_desolve[match(xv[1:6], x), 2]), col.names="rk4.deSolve")
> df <- cbind(df, dfi)
>
> system.time(for (i in 1:10000)
+ lsoda(func = dydt.Gompertz,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01)))
utilisateur système écoulé
19.584 0.187 19.873
> points(x = rk4_desolve[, 1], rk4_desolve[, 2], pch=4)
>
> legend("bottomright",
+ legend=c("Gompertz",
+ "Runge-Kutta by M. Jacquemin",
+ "lsoda from deSolve package"),
+ lty=c(1, 0, 0),
+ pch=c(NA, 1, 4))
>
> df
time Gompertz dy.50 dy.20 dy.10 dy.5 dy.2 dy.1 dy.0.5 dy.0.1
1 0 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000
2 10 2.345293 NA NA 2.274837 2.307908 2.329776 2.337436 2.341340 2.344499
3 20 3.137954 NA 2.849674 2.977788 3.053283 3.102904 3.120225 3.129038 3.136163
4 30 4.083785 NA NA 3.817775 3.943819 4.026034 4.054608 4.069120 4.080839
5 40 5.183115 NA 4.482434 4.799842 4.982534 5.100656 5.141509 5.162217 5.178921
6 50 6.430829 4.574186 NA 5.924656 6.167470 6.322978 6.376483 6.403551 6.425356
rk4 rk4.deSolve
1 1.700000 1.700000
2 2.345268 2.345291
3 3.137904 3.137951
4 4.083711 4.083781
5 5.183020 5.183114
6 6.430713 6.430834
The code for Runge-Kutta algorithm has been done by Maxime Jacquemin (ESE, University Paris Sud). It does a little bit better that the deSolve code but very little.
> # from package embryogrowth
> # function lsoda wants a list
> dydt.Gompertz <- function(t, size, parms) {
+ dy.dt <- parms["alpha"]*log(parms["K"]/size)*size
+ list(dy.dt)
+ }
>
> # Same function but returns a vector
> dydt.Gompertz_2 <- function(t, size, parms) {
+ dy.dt <- parms["alpha"]*log(parms["K"]/size)*size
+ dy.dt
+ }
>
> # Integration of Gompertz function
> Gompertz <- function(x, y0, K, alpha) {
+ return(K*exp(log(y0/K)*exp(-alpha*x)))
+ }
>
> # Fonction d'intégration numérique par la méthode de Runge-Kutta
> # par Maxime Jacquemin
> Runge.Kutta <- function(y, times, func, parms = NULL)
+ {
+ n.iter <- length(times)
+ results <- rep(y, n.iter)
+ yn <- y
+
+ for (i in 2:n.iter)
+ {
+ h <- times[i] - times[i-1]
+ tn <- times[i - 1]
+ k1 <- func(tn, yn, parms)
+ k2 <- func(tn + (h / 2), yn + (h / 2) * k1, parms)
+ k3 <- func(tn + (h / 2), yn + (h / 2) * k2, parms)
+ k4 <- func(tn + h, yn + h * k3, parms)
+ yn <- yn + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4)
+ results[i] <- yn
+ }
+
+ return(data.frame(times, results))
+ }
>
> xv <- seq(from=0, to =500, by=10)
> yv <- Gompertz(xv, y0=1.7, K=50, alpha=0.01)
>
> plot(x = xv,
+ y = yv,
+ type="l", bty="n", xlab="Time", ylab="Value", las=1)
> df <- data.frame(time=xv[1:6], Gompertz=yv[1:6])
>
> # using the approximation dy/dx when dx -> 0
> index <- 1
> for (dy in c(50, 20, 10, 5, 2, 1, 0.5, 0.1)) {
+ x <- seq(from=0, to =500, by=dy)
+ y <- rep(1.7, length(x))
+ for (i in 2:length(x))
+ y[i] <- y[i-1] + dydt.Gompertz_2(x[i], y[i-1], parms=c(K=50, alpha=0.01))*dy
+ dfi <- as.data.frame(list(y[match(xv[1:6], x)]), col.names=paste0("dy.", as.character(dy)))
+ df <- cbind(df, dfi)
+ lines(x, y, col=index)
+ index <- index + 1
+ # text(501, tail(y, 1)+1, as.character(dy), pos=4, xpd=TRUE)
+ }
>
> legend("bottomright", legend=as.character(c(50, 20, 10, 5, 2, 1, 0.5, 0.1)),
+ col=1:8, lty=1, title="dy")
>
> plot(x = xv,
+ y = yv,
+ type="l", bty="n", xlab="Time", ylab="Value", las=1)
>
> dy <- 10
> x <- seq(from=0, to =500, by=dy)
> rk4 <- Runge.Kutta(func = dydt.Gompertz_2,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01)
+ )
> dfi <- as.data.frame(
+ list(
+ rk4[
+ match(xv[1:6], x)
+ , 2]
+ ), col.names="rk4")
> df <- cbind(df, dfi)
>
>
> system.time(for (i in 1:10000)
+ Runge.Kutta(func = dydt.Gompertz_2,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01)
+ )
+ )
utilisateur système écoulé
19.460 0.197 19.766
> points(rk4[, 1], rk4[, 2], pch=1)
>
>
> library(deSolve)
> dy <- 10
> x <- seq(from=0, to =500, by=dy)
> rk4_desolve <- lsoda(func = dydt.Gompertz,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01))
> dfi <- as.data.frame(list(rk4_desolve[match(xv[1:6], x), 2]), col.names="rk4.deSolve")
> df <- cbind(df, dfi)
>
> system.time(for (i in 1:10000)
+ lsoda(func = dydt.Gompertz,
+ times=x,
+ y=1.7,
+ parms=c(K=50, alpha=0.01)))
utilisateur système écoulé
19.584 0.187 19.873
> points(x = rk4_desolve[, 1], rk4_desolve[, 2], pch=4)
>
> legend("bottomright",
+ legend=c("Gompertz",
+ "Runge-Kutta by M. Jacquemin",
+ "lsoda from deSolve package"),
+ lty=c(1, 0, 0),
+ pch=c(NA, 1, 4))
>
> df
time Gompertz dy.50 dy.20 dy.10 dy.5 dy.2 dy.1 dy.0.5 dy.0.1
1 0 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000 1.700000
2 10 2.345293 NA NA 2.274837 2.307908 2.329776 2.337436 2.341340 2.344499
3 20 3.137954 NA 2.849674 2.977788 3.053283 3.102904 3.120225 3.129038 3.136163
4 30 4.083785 NA NA 3.817775 3.943819 4.026034 4.054608 4.069120 4.080839
5 40 5.183115 NA 4.482434 4.799842 4.982534 5.100656 5.141509 5.162217 5.178921
6 50 6.430829 4.574186 NA 5.924656 6.167470 6.322978 6.376483 6.403551 6.425356
rk4 rk4.deSolve
1 1.700000 1.700000
2 2.345268 2.345291
3 3.137904 3.137951
4 4.083711 4.083781
5 5.183020 5.183114
6 6.430713 6.430834


Commentaires
Enregistrer un commentaire