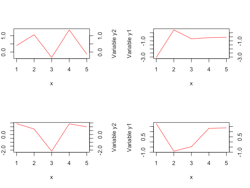
plot with broken y-axis
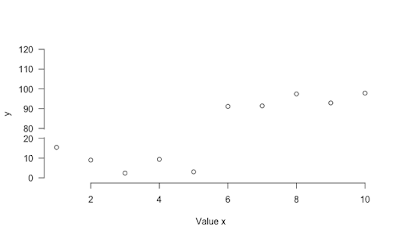
Here is a function to implement broken y-axis. Several enhancements could be done to make it nicer but it works. However it was not fully tested.
A blog about biostatistics using R by Professor Marc Girondot, University Paris Saclay. Subjects can be wide, from ecology to molecular phylogeny or statistics or just tricks to make life easier in R.