Confidence interval of 0 observations with Poisson distribution

https://stats.stackexchange.com/questions/427019/confidence-interval-for-mean-of-poisson-with-only-zero-counts

Excellent answer in this link about the confidence interval when only 0 observations are available for a Poisson distribution.

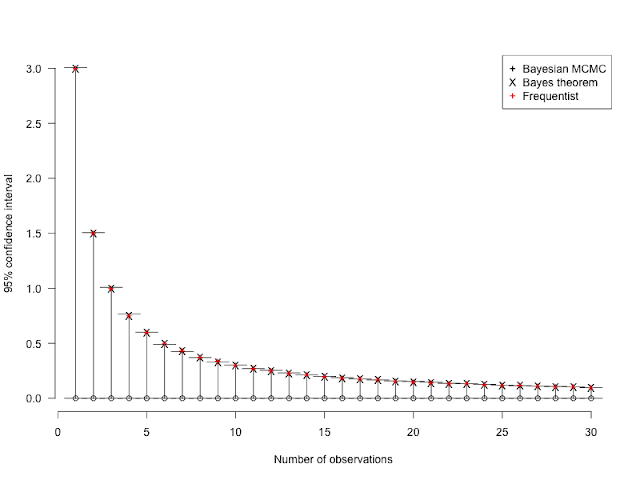
 Here is an alternative using Bayesian MCMC with uniform distribution.

 This is surprising how close are the estimates !

library(HelpersMG)
u <- NULL

for (l in 1:30) {
  val <- rep(0, l)
  prior <- data.frame(Density="dunif",
                      Prior1=0, Prior2=10,
                      SDProp=1,
                      Min=0, Max=10,
                      Init=0.01, row.names = "lambda")
  mcmc_run <- MHalgoGen(n.iter=100000, parameters=prior, data=val, adaptive = TRUE,
                        likelihood=dpoisx, n.chains=1, n.adapt=10000, thin=10, trace=FALSE)
  u <- c(u, quantile(mcmc_run$resultMCMC$"1"[, "lambda"], probs=0.95))
}

plot_errbar(1:30, rep(0, 30), y.minus=rep(0, 30), y.plus = u, las=1, bty="n",
            xlab="Number of observations", ylab="95% confidence interval", ylim=c(0, 3))

points(1:30, qgamma(.95, shape = 1, rate = 1:30), pch="X")
points(1:30, -log(.05)/(1:30), pch="+", col="red")

legend(x = "topright", pch=c("+", "X", "+"), col=c("black", "black", "red"),
       legend = c("Bayesian MCMC", "Bayes theorem", "Frequentist"))


Commentaires

Enregistrer un commentaire

Posts les plus consultés de ce blog

Standard error from Hessian Matrix... what can be done when problem occurs

An Hessian matrix is a square matrix of partial second order derivative. From the square-root of the inverse of the diagonal, it is possible to estimate the standard error of parameters. Let take an example: val=rnorm(100, mean=20, sd=5) # Return -ln L of values in val in Gaussian distribution with mean and sd in par fitnorm<-function(par, val) {   -sum(dnorm(val, par["mean"], par["sd"], log = TRUE)) } # Initial values for search p<-c(mean=20, sd=5) # fit the model result <- optim(par=p, fn=fitnorm, val=val, method="BFGS", hessian=TRUE) # Inverse the hessian matrix to get SE for each parameters mathessian <- result$hessian inversemathessian <- solve(mathessian) res <- sqrt(diag(inversemathessian)) # results data.frame(Mean=result$par, SE=res)   library(MASS) (r<-fitdistr(val, "normal")) It works well. However, the inverse of the matrix cannot be calculated if the second order derivative for some paramete...
Lire la suite

Install treemix in ubuntu 20.04

Informations are available here  https://bitbucket.org/nygcresearch/treemix/downloads/ In terminal, enter for  Ubuntu 20.04: wget https://bitbucket.org/nygcresearch/treemix/downloads/treemix-1.13.tar.gz tar -xvf treemix-1.13.tar.gz sudo apt-get install libgsl-dev sudo apt install libboost-dev sudo apt install libboost-all-dev cd treemix-1.13/ ./configure make sudo make install And it works: $ treemix TreeMix v. 1.13 $Revision: 231 $ Options: -h display this help -i [file name] input file -o [stem] output stem (will be [stem].treeout.gz, [stem].cov.gz, [stem].modelcov.gz) -k [int] number of SNPs per block for estimation of covariance matrix (1) -global Do a round of global rearrangements after adding all populations -tf [file name] Read the tree topology from a file, rather than estimating it -m [int] number of migration edges to add (0) -root [string] comma-delimited list of populations to set on one side of the root (for migration) -g [vertices file name] [edges file na...
Lire la suite

stepAIC from package MASS with AICc

Due to a bug in dropterm() and addterm() in package MASS, it is impossible to use AICc with stepAIC() . Here is a solution. Enter these commands and now you can use: stepAIC(g0, criteria="AICc") or stepAIC(g0, criteria="BIC") For example: datax <- data.frame(y=rnorm(100), x1=rnorm(100),                     x2=rnorm(100), x3=rnorm(100), x4=rnorm(100)) g0 <- glm(y ~ x1+x2+x3+x4, data=datax) gx_AICc <- stepAIC(g0, criteria="AICc") gx_AIC <- stepAIC(g0, criteria="AIC") gx_AIC <- stepAIC(g0, criteria="BIC")
Lire la suite