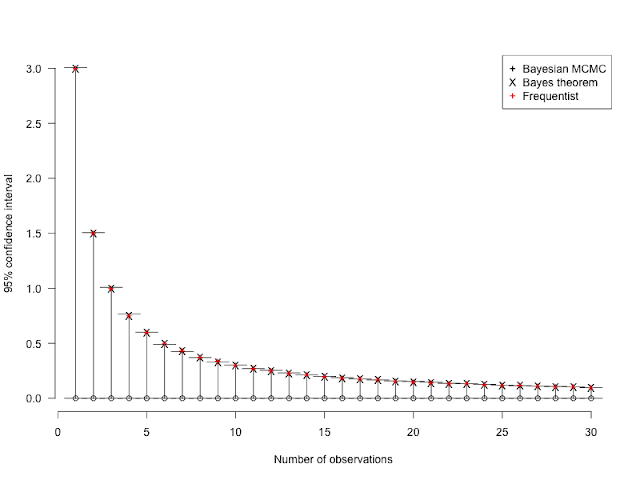
Generate random distribution of truncated distribution
Imagine that you have estimated a sex ratio being 0.8 SE 0.2 by maximum likelihood. If you want make an histogram showing this distribution, the first idea is to do: > sr <- rnorm(100000, mean=0.8, sd=0.2) > sd(sr) [1] 0.2001526 > hist(sr) > sum(sr>1) [1] 15680 > sum(sr<0) [1] 3 The sd of sr is right 0.2 but clearly, it is not correct ! Let do a truncation: > sr <- sr[(sr>0) & (sr<1)] > hist(sr) > length(sr) [1] 84317 > sd(sr) [1] 0.1591352 The histogram is correct but the standard deviation is less than 0.2 due to the truncation. > sfinal <- NULL > x <- seq(from=1E-6, to=1, length.out = 100) > for (sigma in x) + sfinal <- c(sfinal, abs(sd(sin(rnorm(100000, mean=2*asin(sqrt(0.8)), sd=sigma)/2)^2) - 0.2)) > plot(x, sfinal, type="l") > sigma <- x[which.min(sfinal)] > distribution_sr <- sin(rnorm(100000, mean=2*asin(sqrt(0.8)), sd=sigma)/2)^2 > hist(distribution_s...